本文主要从两个方向介绍,一种是基于射影变换的月球表面环境构建;另一种是基于高度图的三维仿真环境构建,目前两种方式都已经实现。本文将引导读者从获取数据集开始完成对月球表面的三维环境构建仿真。
构建仿真文件
在构建三维表面环境的配置中,需要加入一系列的模型文件、配置文件以及发布文件,整个过程对于ROS新手而言是非常晦涩的,我反正一开始就弄糊涂了,不知道文件与文件之间的层级关系。在这里首先给一个大概的概念。ROS的发布文件.launch是相当于可执行文件一样的存在,即是可以直接运行的程序 ,类比于Linux系统下的.sh文件。发布文件中将包含一系列的配置文件以及配置参数,相当于.sh中的一系列参数与函数,因此配置文件相当于不完整的.sh文件,而模型文件只存在于配置文件的调用中,通常不通过发布文件直接调用它。
获取原始数据
无论是三维仿真环境抑或是二维的射影变换仿真,都需要获取较高精度的月球表面遥感图像,目前能够获取到的、开源且较为完整的月球表面数据集是NASA的月球表面数字高程图 和月球表面去除阴影的地形照片 ,分别从对应的路径下载即可,推荐使用IDM 或者XDM 等并发下载器下载,源文件较大,单点下载极慢。
对于去除阴影的遥感地形图,官网上提供有该地形照片的描述文件 和PDS格式说明文件 。查阅描述文件可知,该.tif文件共有以下组成成分:
项目
数值
文件总字节数
11,325,604,841
文件标签字节数
984,041
文件行数
61,440
文件列数
184,320
文件数据类型
8位无符号整数
因此,理论上该文件可以直接使用PIL或者matplotlib等库文件读取,但是由于文件过于巨大,读取存放在内存中极占资源,导致运行速度变慢,且这样做是没有必要的。可以采取流式读取的方式完成数据提取,这里,以960 行作为一个单元,逐单元读取,然后拆分为192个960 × 960 960\times 960 960 × 960 64 × 192 = 12288 64\times 192=12288 64 × 192 = 12288
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 import numpy as npimport matplotlib.pyplot as pltimport tqdmimport osif __name__ == "__main__" : path = "/path/to/your/Lunar_LRO_LOLAKaguya_Shade_60N60S_512ppd.tif" output_dir = ( "/path/to/your/output" ) LABEL_BYTES = 984003 BYTES_PER_PIXEL = 1 LINES = 61440 LINE_SAMPLES = 184320 base_batch = 960 num_batches = LINES // base_batch num_samples = LINE_SAMPLES // base_batch print ( f"The basic batch of DEM is {base_batch} x{base_batch} . Each line contains {num_samples} batches. There are totally {num_batches*num_samples} basic batches." ) with open (path, "rb" ) as f: line = f.read(LABEL_BYTES) for row in tqdm.tqdm(range (num_batches)): data = f.read(LINE_SAMPLES * BYTES_PER_PIXEL * base_batch) data_array = np.frombuffer(data, dtype=np.uint8).reshape( base_batch, LINE_SAMPLES )
同理,如果要处理深度图,同样获取对应的描述文件和格式文件,查阅得知除了单位像素的数据位数不同以外,其余与地形图都完全相同。只需要将位深BYTES_PER_PIXEL取为2,并将数据类型转换为np.uint16,即可完成深度图的逐块读取。
取得地形图后,可以直接使用matplotlib完成对单元块的输出,如下所示:
1 2 3 4 5 6 7 8 9 10 plt.imsave( os.path.join( output_dir, "textures" , f"{row} " , f"txr_{row} _{col} _{base_batch} .png" , ), img_array, cmap="gray" , )
这样,就可以完成对地形图的输出,然后可以在gazebo环境中编辑需要加载的地形照片,以完成仿真环境的搭建,得到的子地形图如下所示:
深度图转三维模型
本部分内容仅针对需要构建三维仿真环境的需求而言,如不需要构建三维仿真环境,则完全可以跳过本部分内容。
基于平面直角坐标
深度图,尤其是二维的深度图可以直接通过三维点的面片拟合完成模型构建,numpy-stl库提供了简单的三维模型操作指令,可用于构建简单的stl模型。请提前确保numpy-stl库已经安装到位。在前文提到的原始960 × 960 960\times 960 960 × 960
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 def make3d (img_array, filename, base_batch=960 , scale_factor=59 ): ''' convert the depth map into a 3D model :param img_array: depth map ndarray :param filename: output filename :param base_batch: the basic size of depth map :param scale_factor: scale factor ''' from stl import mesh x = np.arange(0 , base_batch, 1 ) y = np.arange(0 , base_batch, 1 ) X, Y = np.meshgrid(x, y) Z = img_array / scale_factor num_vertices = base_batch * base_batch num_faces = 2 * (base_batch - 1 ) * (base_batch - 1 ) vertices = np.zeros((num_vertices, 3 )) vertices[:, 0 ] = X.flatten() vertices[:, 1 ] = Y.flatten() vertices[:, 2 ] = Z.flatten() faces = [] for i in range (base_batch - 1 ): for j in range (base_batch - 1 ): faces.append( [ i * base_batch + j, (i + 1 ) * base_batch + j + 1 , (i + 1 ) * base_batch + j, ] ) faces.append( [ i * base_batch + j, i * base_batch + j + 1 , (i + 1 ) * base_batch + j + 1 , ] ) surface_mesh = mesh.Mesh(np.zeros(num_faces, dtype=mesh.Mesh.dtype)) for i, f in enumerate (faces): for j in range (3 ): surface_mesh.vectors[i][j] = vertices[f[j], :] surface_mesh.save(filename)
其中注释部分的内容是用于生成带有底座的三维模型,以方便进一步使用(例如三维打印等),不带注释将生成不带有底座的曲面片(厚度为零),所得的stl文件更小,方便仿真。其中的scale_factor参数是根据深度图或者地形图单个像素长度对应的真实长度的比例尺,为了保证得到的三维模型是原始模型的倍缩模型,必须在宽高和深度三个方向上都保持相同的比例关系。这里,深度图和地形图的的比例尺是1 pixel : 59 m,因此scale_factor取59。使用渲染软件Meshlab可视化得到的模型如下所示:主程序 中加入以下代码:
1 2 3 4 5 6 7 8 9 10 11 make3d( img_array, os.path.join( output_dir, "models" , f"{row} " , f"model_{row} _{col} _{base_batch} .stl" , ), base_batch=base_batch, scale_factor=59 , )
即可生成对应单元块的三维模型,这样就完成了对深度图的三维模型构建。
另一个值得注意的点是,stl模型由一系列三角形面元拼接而成,其文件数据结构是存储的各点深度以及各点构建的三角面元顺序关系。当三角面元的顶点顺序为顺时针时,面元被视为正面,反之被视为背面。而背面的模型在某些渲染引擎中将是不可见的(例如gazebo),如下图所示:
所有 的三角面元的顶点顺序都必须是相同的,否则模型将无法正确显示。
基于球坐标
考虑月球表面的曲率修正后,使用极坐标+双三次线性内插完成模型构建,修改make3d函数如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 from scipy.interpolate import RectBivariateSplinedef make3d ( dem_image, row, col, radius, theta_start, delta_theta, phi_start, delta_phi, padding, output_path, vertices = [] num_steps = dem_image.shape[0 ] x = np.arange(0 , num_steps) y = np.arange(0 , num_steps) f = RectBivariateSpline(x, y, dem_image / scale_factor) for i in range (num_steps): for j in range (num_steps): theta = theta_start - i / num_steps * delta_theta phi = phi_start + j / num_steps * delta_phi xnew, ynew = sphere2plane(theta, phi) r = ( f( xnew - row * (num_steps - pre_padding[0 ]), ynew - col * (num_steps - pre_padding[1 ]), )[0 , 0 ] + radius ) x = r * cos(theta) * cos(phi) y = r * cos(theta) * sin(phi) z = r * sin(theta) vertices.append((x, y, z)) faces = [] for i in range (num_steps - 1 ): for j in range (num_steps - 1 ): current = i * num_steps + j next_theta = current + num_steps faces.append([current, next_theta, current + 1 ]) faces.append([current + 1 , next_theta, next_theta + 1 ]) sphere_segment = mesh.Mesh(np.zeros(len (faces), dtype=mesh.Mesh.dtype)) for i, f in enumerate (faces): for j in range (3 ): sphere_segment.vectors[i][j] = vertices[f[j]] sphere_segment.save(output_path)
辅助函数执行等距圆柱投影将经纬度转平面图坐标:
1 2 3 4 5 6 7 8 9 def sphere2plane (lat, lon ): """ Warning ! The unit of latitude and longitude is degree. """ x = (lat - pi / 6 ) * X_PIXEL_RANGE / LATITUDE_RANGE y = lon * Y_PIXEL_RANGE / LONGITUDE_RANGE return x, y
完成曲率修正后,实际上还遇到一个问题:面片与面片之间存在接缝,如图所示:
[{"url":"面片接缝示意图1.png","alt":"面片接缝示意图1"},{"url":"面片接缝示意图2.png","alt":"面片接缝示意图2"},{"url":"面片接缝示意图3.png","alt":"面片接缝示意图3"},{"url":"面片接缝示意图4.png","alt":"面片接缝示意图4"}]
可见中间的灰色接缝 事实上是空的,不同于面片上存在的缝状图形。该接缝存在的原因来自于:任意两块相邻的面片之间的DEM图没有关联。由于制作stl模型是按照直角坐标或者极坐标(实际上还是直角坐标)遍历面片上现有的全部像素点,将三个紧接的像素顶点作为三角形面元完成模型构建,但是不同的面片之间的像素点没有三角形面元产生,因此在不同的面片之间就形成了1个像素宽的接缝。解决该接缝的办法也比较直白:使用滑动窗口法。本模型使用极坐标构建,因此坐标满足旋转对称性,使用滑动窗口法带来的多余边角不会凸起于表面。将主程序入口修改为:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 with open (path, "rb" ) as f: line = f.read(LABEL_BYTES) theta_start = pi / 6 phi_start = 0 for row in tqdm.tqdm(range (num_batches)): if row == 0 : data = f.read(LINE_SAMPLES * BYTES_PER_PIXEL * (base_batch + 1 )) data_array = np.frombuffer(data, dtype=np.int16).reshape( base_batch + 1 , LINE_SAMPLES ) strip = data_array[-1 , :] elif row == num_batches - 1 : data = f.read(LINE_SAMPLES * BYTES_PER_PIXEL * (base_batch - 1 )) strip = data_array[-2 :, :] data_array = np.frombuffer(data, dtype=np.int16).reshape( base_batch + 1 , LINE_SAMPLES ) data_array = np.vstack((strip, data_array)) theta_start -= delta_theta * 2 else : data = f.read(LINE_SAMPLES * BYTES_PER_PIXEL * base_batch) strip = data_array[-1 , :] data_array = np.frombuffer(data, dtype=np.int16).reshape( base_batch + 1 , LINE_SAMPLES ) data_array = np.vstack((strip, data_array)) theta_start -= delta_theta if not os.path.exists(os.path.join(output_dir, "dem_int16" )): os.makedirs(os.path.join(output_dir, "dem_int16" )) if not os.path.exists(os.path.join(output_dir, "stl_models" )): os.makedirs(os.path.join(output_dir, "stl_models" )) if not os.path.exists(os.path.join(output_dir, "dem_int16" , f"{row} " )): os.makedirs(os.path.join(output_dir, "dem_int16" , f"{row} " )) if not os.path.exists(os.path.join(output_dir, "stl_models" , f"{row} " )): os.makedirs(os.path.join(output_dir, "stl_models" , f"{row} " )) for col in range (num_samples): if col == num_samples - 1 : img_array = data_array[ :, col * base_batch - 1 : (col + 1 ) * base_batch ] phi_start -= delta_phi else : img_array = data_array[ :, col * base_batch : (col + 1 ) * base_batch + 1 ] theta_start += delta_theta * row phi_start += delta_phi * col create_sphere_segment( img_array, row, col, radius, theta_start, delta_theta, phi_start, delta_phi, 1 , os.path.join( output_dir, "stl_models" , f"{row} " , f"{row} _{col} _{base_batch} .stl" , ), )
到此可以完成丝滑地曲面月球三维模型构建。
构建三维世界
同样地,如果不需要完成三维仿真环境构建,只需要跳过本部分即可。如果需要将构建得到的三维模型加入至gazebo仿真环境中,首先需要在模型文件夹Tools/sitl_gazebo/models内新建模型,例如,将该模型命名为moon_surface_3d,其中文件的结构如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 moon_surface_3d ├── materials │ └── textures │ ├── txr_0_0_960.png │ ├── txr_0_1_960.png │ ├── txr_1_0_960.png | └── ... ├── meshes │ ├── 0_0_960.stl │ ├── 0_1_960.stl │ ├── 1_0_960.stl | └── ... ├── model.config └── moon.sdf
其中的textures子文件夹存放的是用于贴图的纹理文件,就是深度图对应位置处的去阴影地形图,该文件可以用于获取更加真实的视觉模型体验。打开新建的model.sdf文件,加入的内容如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 <?xml version="1.0" ?> <sdf version ="1.4" > <model name ="moon_surface_3d" > <static > true</static > <link name ="link" > <collision name ="collision_0_0" > <geometry > <mesh > <uri > model://moon_surface_3d/meshes/0_0_960.stl</uri > <scale > 0.1 0.1 0.1</scale > </mesh > </geometry > </collision > <visual name ="visual_0_0" > <geometry > <mesh > <uri > model://moon_surface_3d/meshes/0_0_960.stl</uri > <scale > 0.1 0.1 0.1</scale > </mesh > </geometry > <material > <ambient > 0.5 0.5 0.5 1</ambient > <diffuse > 0.5 0.5 0.5 1</diffuse > <script > <uri > model://moon_surface_3d/materials/textures/txr_0_0_960.png</uri > <name > MoonSurface/Diffuse_0_0</name > </script > </material > </visual > <collision name ="collision_0_1" > <geometry > <pose > 100 0 0 0 0 0</pose > <mesh > <uri > model://moon_surface_3d/meshes/0_1_960.stl</uri > <scale > 0.1 0.1 0.1</scale > </mesh > </geometry > </collision > <visual name ="visual_0_1" > <pose > 100 0 0 0 0 0</pose > <geometry > <mesh > <uri > model://moon_surface_3d/meshes/0_1_960.stl</uri > <scale > 0.1 0.1 0.1</scale > </mesh > </geometry > <material > <ambient > 0.5 0.5 0.5 1</ambient > <diffuse > 0.5 0.5 0.5 1</diffuse > <script > <uri > model://moon_surface_3d/materials/textures/txr_0_1_960.png</uri > <name > MoonSurface/Diffuse_0_1</name > </script > </material > </visual > </link > </model > </sdf >
在model.config文件中加入如下内容:
1 2 3 4 5 6 7 8 9 10 11 12 <?xml version="1.0" ?> <model > <name > moon_surface_3d</name > <version > 1.0</version > <sdf > moon.sdf</sdf > <author > <name > Your name</name > </author > <description > A simple moon surface model </description > </model >
然后按照文件目录要求放入对应的纹理文件和模型文件,在Tools/sitl_gazebo/worlds文件夹中新建一个moon_surface_3d.world文件,加入如下内容:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 <?xml version="1.0" ?> <sdf version ="1.5" > <world name ="default" > <include > <uri > model://sun</uri > </include > <include > <name > moon part 0 67</name > <uri > model://moon_surface_3d</uri > <pose > 0 0 0 0 0 0</pose > </include > <physics name ='default_physics' default ='0' type ='ode' > <gravity > 0 0 -9.8066</gravity > <ode > <solver > <type > quick</type > <iters > 10</iters > <sor > 1.3</sor > <use_dynamic_moi_rescaling > 0</use_dynamic_moi_rescaling > </solver > <constraints > <cfm > 0</cfm > <erp > 0.2</erp > <contact_max_correcting_vel > 100</contact_max_correcting_vel > <contact_surface_layer > 0.001</contact_surface_layer > </constraints > </ode > <max_step_size > 0.002</max_step_size > <real_time_factor > 1</real_time_factor > <real_time_update_rate > 500</real_time_update_rate > <magnetic_field > 6.0e-6 2.3e-5 -4.2e-5</magnetic_field > </physics > <light name ="moon_surface_3d_light" type ="directional" > <cast_shadows > false</cast_shadows > <pose > 0 0 100 0 0.8 0.2</pose > <diffuse > 0.8 0.8 0.8 1</diffuse > <specular > 0.2 0.2 0.2 1</specular > <attenuation > <range > 1000</range > <constant > 0.9</constant > <linear > 0.01</linear > <quadratic > 0.001</quadratic > </attenuation > <direction > -0.5 0.1 -0.9</direction > </light > </world > </sdf >
这里的各项参数可以根据实际情况调整,注意,模型光照选项<cast_shadows>被关闭是因为,gazebo自带的阴影效果实在是惨不忍睹,还不如不要,因此将其显式关闭。如需要添加更多的单位面元,请在上述配置文件中按相同的形式复制粘贴并修改名字即可。至此,三维仿真世界的环境构建工作就完成了。
模型姿态问题
这里实质上没有提到一个重要的问题:模型姿态。理想情况下是将全部模型的全部球面片一起加入至内存中,然后直接让无人机在球面的引力场中绕月飞行并着陆。
实际上一个也做不到,首先内存和处理器的性能不够,全部球面片的占用空间高达1145141081344 M B ≈ 1.03 T B 1081344\mathrm{MB}\approx 1.03\mathrm{TB} 1081344 MB ≈ 1.03 TB
球面片加载不全,那就只加载一部分,合理的;
重力方向不能修改,幸好月球比较大,在局部地区上,可以视为重力场是竖直向下的,因此无人机不需要额外附加力改变其姿态。
因此问题得以简化为:每次只输入一部分(经测试最多15块)球面片构建局部月表,无人机在该局部月表上空飞行拍摄图像,新的问题出现了:如何将不同的球面片构建为相同位置处的局部月表,或者说,如何保证原点在每个场景中根据需要改变,以保证无人机获取的图像信息能够用位姿去解算并查阅陨石坑表格。这需要知道Gazebo仿真环境中的<pose>标签含义。文档强调:<pose>x y z w_x w_y w_z<pose>中前三项是三轴位置坐标,后三项分别是物体三轴欧拉角 ,一定注意不是绕三轴的旋转角度!这一点我被ChatGPT带偏了,正确的解释可参考博客 ,三轴转角和三轴欧拉角的区别在于,三轴转角与先后次序无关,而欧拉角与先后次序有关(且很大),后绕的轴就建立在先绕的坐标系上,因此不同转动次序带来的结果完全不同,即称欧拉轴角的万向锁效应 。
原以为不搞控制就不需要考虑万向锁,看来还是单纯了点
现问题简化为:已知球面上某点的纬度、经度( θ , ϕ ) (\theta,\phi) ( θ , ϕ ) ( 0 , 0 , 1 ) (0,0,1) ( 0 , 0 , 1 )
[ cos θ cos ϕ cos θ sin ϕ sin θ ] = R ( α , β , γ ) [ 0 0 1 ] \begin{bmatrix}
\cos\theta\cos\phi\\
\cos\theta\sin\phi\\
\sin\theta
\end{bmatrix}=\mathbf{R}(\alpha,\beta,\gamma)\begin{bmatrix}
0\\
0\\
1
\end{bmatrix}
cos θ cos ϕ cos θ sin ϕ sin θ = R ( α , β , γ ) 0 0 1
其中三个角度α , β , θ \alpha,\beta,\theta α , β , θ x , y , z x,y,z x , y , z R ( α , β , γ ) \mathbf{R}(\alpha,\beta,\gamma) R ( α , β , γ ) 球面坐标 !!因此解析解的表示结果可以直接凑出来:
R = [ sin θ 0 − cos θ 0 1 0 cos θ 0 sin θ ] [ cos ϕ sin ϕ 0 − sin ϕ cos ϕ 0 0 0 1 ] \mathbf{R}=\begin{bmatrix}
\sin\theta&0&-\cos\theta\\
0&1&0\\
\cos\theta&0&\sin\theta
\end{bmatrix}\begin{bmatrix}
\cos\phi&\sin\phi&0\\
-\sin\phi&\cos\phi&0\\
0&0&1
\end{bmatrix}
R = sin θ 0 cos θ 0 1 0 − cos θ 0 sin θ cos ϕ − sin ϕ 0 sin ϕ cos ϕ 0 0 0 1
验证其能够将球面上的点变换为北极点:
[ sin θ 0 − cos θ 0 1 0 cos θ 0 sin θ ] [ cos ϕ sin ϕ 0 − sin ϕ cos ϕ 0 0 0 1 ] [ cos θ cos ϕ cos θ sin ϕ sin θ ] = [ sin θ 0 − cos θ 0 1 0 cos θ 0 sin θ ] [ cos θ 0 sin θ ] = [ 0 0 1 ] \begin{bmatrix}
\sin\theta&0&-\cos\theta\\
0&1&0\\
\cos\theta&0&\sin\theta
\end{bmatrix}\begin{bmatrix}
\cos\phi&\sin\phi&0\\
-\sin\phi&\cos\phi&0\\
0&0&1
\end{bmatrix}\begin{bmatrix}
\cos\theta\cos\phi\\
\cos\theta\sin\phi\\
\sin\theta
\end{bmatrix}=\begin{bmatrix}
\sin\theta&0&-\cos\theta\\
0&1&0\\
\cos\theta&0&\sin\theta
\end{bmatrix}\begin{bmatrix}
\cos\theta\\
0\\
\sin\theta
\end{bmatrix}=\begin{bmatrix}
0\\
0\\
1
\end{bmatrix}
sin θ 0 cos θ 0 1 0 − cos θ 0 sin θ cos ϕ − sin ϕ 0 sin ϕ cos ϕ 0 0 0 1 cos θ cos ϕ cos θ sin ϕ sin θ = sin θ 0 cos θ 0 1 0 − cos θ 0 sin θ cos θ 0 sin θ = 0 0 1
因此矩阵R \mathbf{R} R 三轴欧拉角 ,这里需要根据旋转矩阵反解欧拉角,这个就好办了。可以直接使用最常见的四象限反正切求解:
α = arctan ( R 32 R 33 ) β = arctan ( − R 31 R 32 2 + R 33 2 ) γ = arctan ( R 21 R 11 ) \begin{aligned}
\alpha&=\arctan\left(\frac{R_{32}}{R_{33}}\right)\\
\beta&=\arctan\left(\frac{-R_{31}}{\sqrt{R_{32}^2+R_{33}^2}}\right)\\
\gamma&=\arctan\left(\frac{R_{21}}{R_{11}}\right)
\end{aligned}
α β γ = arctan ( R 33 R 32 ) = arctan ( R 32 2 + R 33 2 − R 31 ) = arctan ( R 11 R 21 )
由此可知,根据经纬度坐标求解模型姿态的程序代码可编写为如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 def Rotate (ori ): x, y, z = ori R_x = np.array( [ [1 , 0 , 0 ], [0 , cos(x), sin(x)], [0 , -sin(x), cos(x)], ] ) R_y = np.array( [ [cos(y), 0 , -sin(y)], [0 , 1 , 0 ], [sin(y), 0 , cos(y)], ] ) R_z = np.array( [ [cos(z), sin(z), 0 ], [-sin(z), cos(z), 0 ], [0 , 0 , 1 ], ] ) return R_x @ R_y @ R_z R = Rotate([0 , pi/2 - theta, phi]) alpha = atan2(R[2 , 1 ], R[2 , 2 ]) beta = atan2(-R[2 , 0 ], sqrt(R[2 , 1 ] ** 2 + R[2 , 2 ] ** 2 )) gamma = atan2(R[1 , 0 ], R[0 , 0 ]) print ("x, y, z" )print (f"{alpha} ,{beta} ,{gamma} " )
输出结果直接可以填入至SDF文件中,完成月球表面的旋转标准化,然后再减去月球的平均半径,即可将上述月球球面片平移至原点附近,完成初始化设置。
构建二维世界
二维模型的加载与三维模型基本一致,不同之处在于,二维模型不需要加载stl文件,因此其模型文件夹结构如下所示:
1 2 3 4 5 6 7 8 9 10 moon_surface_2d ├── materials │ ├── scripts │ │ └── moon_surface.material │ └── textures │ ├── txr_0_0_960.png │ ├── txr_0_1_960.png │ └── ... ├── model.config └── moon_surface.sdf
有两种方式可以实现对二维地形图像的加载,一种是通过二维地表贴图,即先加臷一个ground_plane模型,然后在该模型上加贴图,另一种则是直接加载二维地形图像,然后设置对二维地形图像的碰撞信息。这里选取的是第二种方式。首先,在moon_surface.sdf文件中写入以下内容:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 <?xml version="1.0" ?> <sdf version ="1.4" > <model name ="moon_surface" > <static > true</static > <link name ="link" > <collision name ="collision_0_0" > <pose > 0 0 0 0 0 0</pose > <geometry > <plane > <normal > 0 0 1</normal > <size > 96 96</size > </plane > </geometry > </collision > <visual name ="visual_0_0" > <pose > 0 0 0 0 0 0</pose > <geometry > <plane > <normal > 0 0 1</normal > <size > 96 96</size > </plane > </geometry > <material > <script > <uri > model://moon_surface/materials/textures/</uri > <uri > model://moon_surface/materials/scripts/</uri > <name > MoonSurface/Diffuse_0_0</name > </script > </material > </visual > <collision name ="collision_0_1" > <pose > 95.9 0 0 0 0 0</pose > <geometry > <plane > <normal > 0 0 1</normal > <size > 96 96</size > </plane > </geometry > </collision > <visual name ="visual_0_1" > <pose > 95.9 0 0 0 0 0</pose > <geometry > <plane > <normal > 0 0 1</normal > <size > 96 96</size > </plane > </geometry > <material > <script > <uri > model://moon_surface/materials/textures/</uri > <uri > model://moon_surface/materials/scripts/</uri > <name > MoonSurface/Diffuse_0_1</name > </script > </material > </visual > </link > </model > </sdf >
在model.config文件中加入如下内容:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 <?xml version="1.0" ?> <model > <name > Ground Plane</name > <version > 1.0</version > <sdf version ="1.6" > moon_surface.sdf</sdf > <author > <name > your model name</name > <email > abcd@buaa.edu.cn</email > </author > <description > A simple moon surface for crater simulation. </description > </model >
注意model.config文件中的<name>标签中的内容必须与sdf文件中的<model>标签中的<name>标签中的内容一致,否则模型无法加载。在materials/scripts文件夹中新建一个moon_surface.material文件,加入如下内容:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 material MoonSurface/Diffuse_0_0 { technique { pass { ambient 1.0 1.0 1.0 1.0 diffuse 1.0 1.0 1.0 1.0 specular 0.0 0.0 0.0 1.0 1.0 texture_unit { texture txr_0_0_960.png filtering trilinear } } } } material MoonSurface/Diffuse_0_1 { technique { pass { ambient 1.0 1.0 1.0 1.0 diffuse 1.0 1.0 1.0 1.0 specular 0.0 0.0 0.0 1.0 1.0 texture_unit { texture txr_0_1_960.png filtering trilinear } } } }
同样,本文件中的material字段的内容也需要与sdf文件中的<material>标签中的<name>标签中的内容一致,否则模型无法加载。如需要添加由更多面片组成更大范围的仿真环境,请在两个文件中按相同的形式ctrl C ctrl V并修改文件名和标签名即可。至此,二维仿真世界的环境构建工作就完成了。
构建世界模型
本步骤需要在Tools/sitl_gazebo/worlds文件中增加一个moon_surface.world文件,加入如下内容:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 <?xml version="1.0" ?> <sdf version ="1.5" > <world name ="default" > <include > <uri > model://sun</uri > </include > <include > <name > moon</name > <uri > model://moon_surface</uri > <pose > 0 0 0 0 0 0</pose > </include > <physics name ='default_physics' default ='0' type ='ode' > <gravity > 0 0 -9.8066</gravity > <ode > <solver > <type > quick</type > <iters > 10</iters > <sor > 1.3</sor > <use_dynamic_moi_rescaling > 0</use_dynamic_moi_rescaling > </solver > <constraints > <cfm > 0</cfm > <erp > 0.2</erp > <contact_max_correcting_vel > 100</contact_max_correcting_vel > <contact_surface_layer > 0.001</contact_surface_layer > </constraints > </ode > <max_step_size > 0.002</max_step_size > <real_time_factor > 1</real_time_factor > <real_time_update_rate > 500</real_time_update_rate > <magnetic_field > 6.0e-6 2.3e-5 -4.2e-5</magnetic_field > </physics > <light name ="moon_surface_light" type ="directional" > <pose > 0 0 100 0 0.8 0.2</pose > <diffuse > 0.8 0.8 0.8 1</diffuse > <specular > 0.2 0.2 0.2 1</specular > <attenuation > <range > 1000</range > <constant > 0.9</constant > <linear > 0.01</linear > <quadratic > 0.001</quadratic > </attenuation > <direction > -0.5 0.1 -0.9</direction > </light > </world > </sdf >
此时的世界模型就可以通过本文件修改其全局的物理参数,如模型的大小、重力加速度或者摩擦系数等,不需要在模型文件中逐个设置。
构建发布文件
最后,需要在Tools/sitl_gazebo/launch文件夹中新建一个moon_surface.launch文件,本文件将含有包括世界模型、加入的无人机模型(包括上面固连的传感器模型)以及其他任何自定义的模型。在该文件中加入如下内容:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 <?xml version="1.0" ?> <launch > <arg name ="x" default ="5" /> <arg name ="y" default ="5" /> <arg name ="z" default ="20" /> <arg name ="R" default ="0" /> <arg name ="P" default ="0" /> <arg name ="Y" default ="0" /> <arg name ="my_model" default ="iris_evt_cam" /> <arg name ="est" default ="ekf2" /> <arg name ="vehicle" default ="iris" /> <arg name ="world" default ="$(find mavlink_sitl_gazebo)/worlds/moon.world" /> <arg name ="sdf" default ="$(find mavlink_sitl_gazebo)/models/$(arg my_model)/$(arg my_model).sdf" /> <arg name ="gui" default ="true" /> <arg name ="debug" default ="false" /> <arg name ="verbose" default ="false" /> <arg name ="paused" default ="false" /> <arg name ="respawn_gazebo" default ="false" /> <arg name ="fcu_url" default ="udp://:14540@localhost:14557" /> <arg name ="respawn_mavros" default ="false" /> <arg name ="interactive" default ="true" /> <include file ="$(find px4)/launch/posix_sitl.launch" > <arg name ="x" value ="$(arg x)" /> <arg name ="y" value ="$(arg y)" /> <arg name ="z" value ="$(arg z)" /> <arg name ="R" value ="$(arg R)" /> <arg name ="P" value ="$(arg P)" /> <arg name ="Y" value ="$(arg Y)" /> <arg name ="world" value ="$(arg world)" /> <arg name ="vehicle" value ="$(arg vehicle)" /> <arg name ="sdf" value ="$(arg sdf)" /> <arg name ="gui" value ="$(arg gui)" /> <arg name ="interactive" value ="$(arg interactive)" /> <arg name ="debug" value ="$(arg debug)" /> <arg name ="verbose" value ="$(arg verbose)" /> <arg name ="paused" value ="$(arg paused)" /> <arg name ="respawn_gazebo" value ="$(arg respawn_gazebo)" /> </include > <include file ="$(find mavros)/launch/px4.launch" > <arg name ="gcs_url" value ="" /> <arg name ="fcu_url" value ="$(arg fcu_url)" /> <arg name ="respawn_mavros" value ="$(arg respawn_mavros)" /> </include > </launch >
至此,所有的文件配置都已经准备就绪。
运行仿真环境
至此激动人心的时刻终于来了,首先请确保所有文件都保存完毕,打开容器的终端,确保自己的catkin_ws工作目录的环境变量和PX4_Autopilot的环境变量都已经激活,然后运行以下命令:
1 roslaunch px4 moon_mavros_posix_sitl.launch
此时将可以看到仿真环境正常加载,如下图所示:
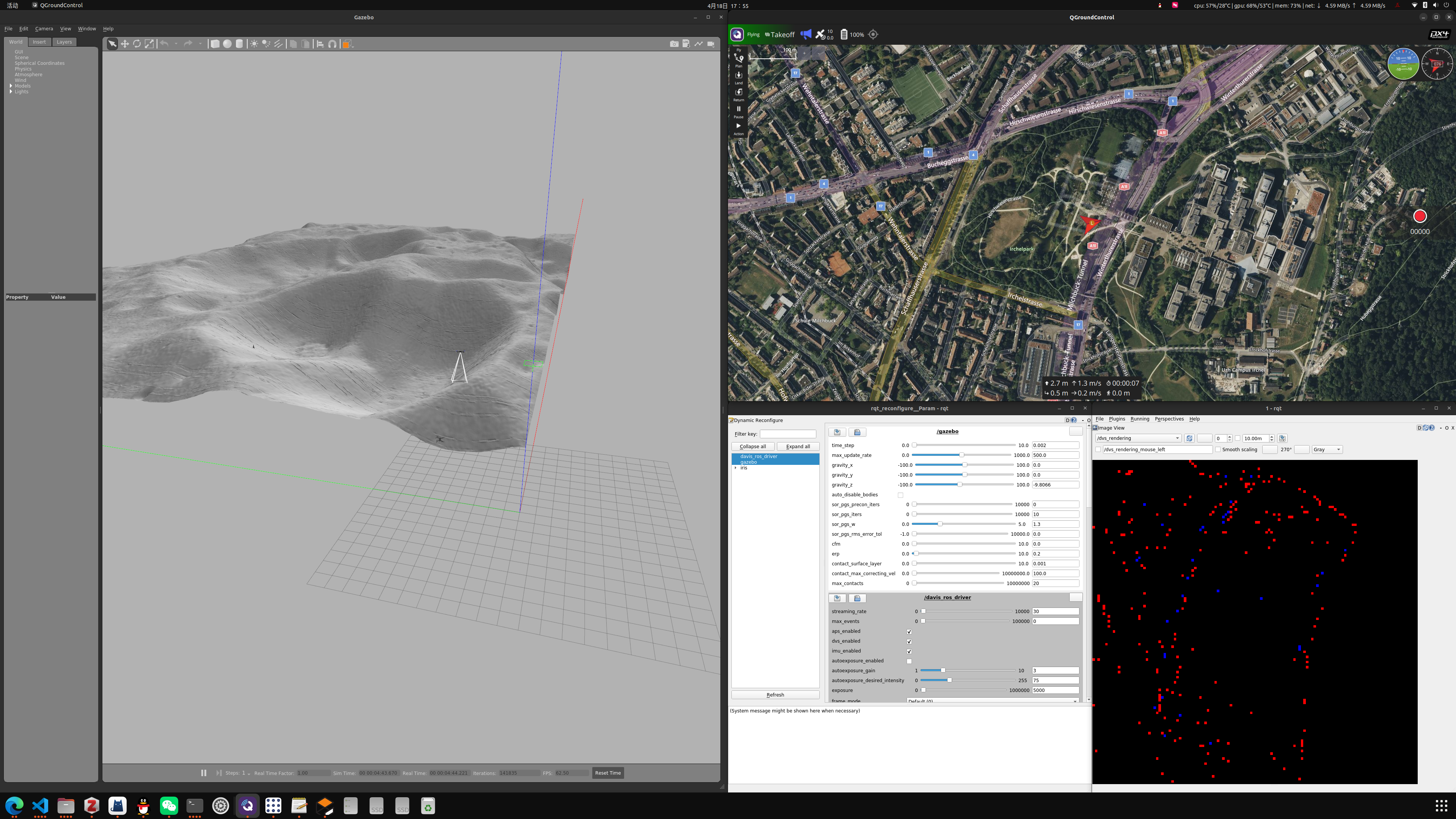
此时将会打开QGroundControl软件,可以通过该软件对无人机进行控制,如下图所示:
1 roslaunch dvs_renderer davis_mono.launch
刚打开时可能该用户界面什么也显示不了,这是因为无人机尚未起飞 ,传感器仍处于关机模式 ,此时需要使用QG控制无人机使其飞行,然后界面将显示可视化后的事件图像,如下所示:
后话
事实上,直接从DEM文件中生成得到的三维模型是不准确的,因为DEM模型在纬度上存在扭曲(真实的陨石坑也很少扁成这样 ),直接构建的stl文件将在纬度上产生失真,且该失真是三维失真,不能够使用射影变换补偿,因此必须严格按照月球表面的球面几何关系,重新构建三维模型。这期间遇到了相当多的技术上的问题,有必要记录一下。
之前直接在平面坐标上用高程信息构建,而球面上无法存在这样的点,且平面上的每个点映射回球面的变换是不均匀的,起初想用球面向平面的投影来构建(那一小片类似于梯形的图形),赤道附近的投影图像接近于零,构建的误差将变得非常大,迫于无奈放弃。幸好放弃了,这个方法推导的通式都不知道有多复杂
然后再考虑是否将球面片向其法向量方向投影,后来也觉得投影结果很复杂,且几何关系难于解算(要反解三角函数,误差越来越大)。百般无头绪之际,请教了ChatGPT ,果然有了好方法!那就是!
应当选用球面坐标系求解三维点线,应有:
{ x = cos θ cos ϕ y = cos θ sin ϕ z = sin θ \left\{
\begin{aligned}
x&=\cos\theta\cos\phi\\
y&=\cos\theta\sin\phi\\
z&=\sin\theta
\end{aligned}
\right.
⎩ ⎨ ⎧ x y z = cos θ cos ϕ = cos θ sin ϕ = sin θ
同样地,球坐标变换结果与平面坐标并不是线性关系,球面按经纬度划分的各点坐标在平面上没有对应关系,一个明显的方法是:
常见的图像内插算法有最近邻内插nearest 、双线性内插bilinear 、双三次线性内插cubic ,最近邻过于锯齿直接pass ,双线性内插尝试过,发现图像插值结果的横竖条纹非常明显(模式非常眼熟,甚至怀疑DEM模型中的条纹就是这么来的 )。双三次线性内插的表达式有些复杂,纠结之际,再次请出ChatGPT请教双三次线性插值的快捷方法,这便是引用scipy.interpolate库中的函数RectBivariateSpline,直接对二维图像内点插值。修改后结果在上文 中已经展示,其中出现了几处细节需要注意:
经纬度范围
1 2 theta = theta_start - i / num_steps * delta_theta phi = phi_start + j / num_steps * delta_phi
单个球面片本来占据2 3 π 1 64 = 120 ∘ 64 \frac{2}{3}\pi\frac{1}{64}=\frac{120^\circ}{64} 3 2 π 64 1 = 64 12 0 ∘ 2 π 192 = 120 ∘ 64 \frac{2\pi}{192}=\frac{120^\circ}{64} 192 2 π = 64 12 0 ∘ 球坐标插值 完成拟合:
1 2 3 4 5 6 7 8 9 10 11 xnew, ynew = sphere2plane(theta, phi) r = ( f( xnew - row * (num_steps - pre_padding[0 ]), ynew - col * (num_steps - pre_padding[1 ]), )[0 , 0 ] + radius ) x = r * cos(theta) * cos(phi) y = r * cos(theta) * sin(phi) z = r * sin(theta)
双三次线性插值后的图像基本平滑,不会产生的新的条纹模式。
接缝问题
虽然插值不产生新的条纹模式,但是球面片与球面片之间并不是完全相连的,当每个球面片在等距圆柱投影图像DEM上的结果是以960 × 960 960\times 960 960 × 960 stl文件时必然会因边界上本片与相邻片没有共享的像素导致模型断开,产生新接缝,如下图所示:
由于DEM图像本身非常巨大(22G),当前设备并不能一下子把它全部读入内存然后处理。因此我采用的是流式读取处理法,即每次读取960行,每行共有184320个16位的像素,可以分为192幅球面片。而python的输入流也是流式的,即所有的数据在缓冲区内只能被读取一次,读取后栈顶指针偏移,下次再读取时指向的不是当前的字节位置。因此在行方向上,不能直接采用滑窗读取过去时刻的内容,(列方向上不受此影响)一个自然的想法是:将前一时刻读取的字节数据缓冲一行,在下一个时刻读取到来之时,再将其与下一时刻读取的字节数据合并。
1 2 3 4 f( xnew - row * (num_steps - pre_padding[0 ]), ynew - col * (num_steps - pre_padding[1 ]), )[0 , 0 ]
这里展示的是正确的脚本程序,其中,nums_steps代表的是合并字节数后的图像像素个数(960+1)。pre_padding变量两个元素分别代表向行、列上的滑窗共享像素数量,这里都是1 。而实际上,如果不加入这一修正滑窗的值,前一时刻合并的字节数量在当前坐标位置下的投影就将小于row * num_steps,即产生了负值坐标。而函数RectBivariateSpline仅能对图像内的点插值,对于超出范围的数据,其采用的是最简单的处理方式以保证程序不出bug,即直接取为边缘像素值。由此,边缘处像素被展平,且随着行数增加,展平的范围也增加(因为row变量增大了,负得越来越多)。解决方法便是加入以上修正量,保证在合并前一时刻数据时,当前图像个数去除了共享像素。
像素位置偏移
本问题有点类似于问题2的接缝问题,也是因为共享像素的位置偏移造成的,这里不体现为图像展平,而是图像像素与上一个时刻相同,但是位置不同(相对于上一个时刻有微小的偏移),原因也比较好辨认,即共享像素带来了1格范围的像素回退,则经纬度范围也应当相应回退1格,在代码中的这部分内容便是解决该问题的:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 if row == 0 : data = f.read(LINE_SAMPLES * BYTES_PER_PIXEL * (base_batch + 1 )) data_array = np.frombuffer(data, dtype=np.int16).reshape( base_batch + 1 , LINE_SAMPLES ) strip = data_array[-1 , :] delta_theta_start = 0 elif row == num_batches - 1 : data = f.read(LINE_SAMPLES * BYTES_PER_PIXEL * (base_batch - 1 )) strip = data_array[-2 :, :] data_array = np.frombuffer(data, dtype=np.int16).reshape( base_batch - 1 , LINE_SAMPLES ) data_array = np.vstack((strip, data_array)) delta_theta_start = -delta_theta * 2 / base_batch else : data = f.read(LINE_SAMPLES * BYTES_PER_PIXEL * base_batch) strip = data_array[-1 , :] data_array = np.frombuffer(data, dtype=np.int16).reshape( base_batch, LINE_SAMPLES ) data_array = np.vstack((strip, data_array)) delta_theta_start = -delta_theta / base_batch
以及解决列方向(经度方向)的像素位置偏移:
1 2 3 4 5 6 7 8 9 10 11 12 13 if col == num_samples - 1 : img_array = data_array[ :, col * base_batch - 1 : (col + 1 ) * base_batch ] delta_phi_start = -delta_phi / base_batch else : img_array = data_array[ :, col * base_batch : (col + 1 ) * base_batch + 1 ] delta_phi_start = 0
由此,可以完成正确的模型生成。实际上也还有最后一点点小问题,即经度方向上最后一片(序号为1)与第1片(序号为0)球面片仍然有接缝,这是因为最后一片球面片取出的是前一时刻列的字节数据(因为右边已经到头了,而其他片都是取的后一个时刻的字节数据),所以与序号为0的球面片实际上没有共享像素。这个问题不太影响结果,我就懒得去改了,要解决它的也比较简单,在列方向的像素位置偏移上,修改代码为如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 if col == num_samples - 1 : img_array = data_array[ :, col * base_batch : (col + 1 ) * base_batch ] temp = data_array[:, 0 ] img_array = np.concatenate([img_array, temp], axis=1 ) delta_phi_start = 0 else : img_array = data_array[ :, col * base_batch : (col + 1 ) * base_batch + 1 ] delta_phi_start = 0
这一修改实质上还可以减少一个变量delta_phi_start,看上去程序也被优化了,似乎更好了。
完整的球面三维模型构建程序放置于下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 from math import sin, cos, pifrom stl import meshimport numpy as npimport osimport tqdmfrom scipy.interpolate import RectBivariateSplineLABEL_BYTES = 984003 BYTES_PER_PIXEL = 2 LINES = 61440 LINE_SAMPLES = 184320 LATITUDE_RANGE = 2 / 3 * pi LONGITUDE_RANGE = 2 * pi X_PIXEL_RANGE = 61440 Y_PIXEL_RANGE = 184320 scale_factor = 59 def sphere2plane (lat, lon ): """ Warning ! The unit of latitude and longitude is degree. """ x = (pi / 3 - lat) * X_PIXEL_RANGE / LATITUDE_RANGE y = lon * Y_PIXEL_RANGE / LONGITUDE_RANGE return x, y def create_sphere_segment ( dem_image, row, col, radius, theta_start, delta_theta, phi_start, delta_phi, pre_padding: list , output_path, vertices = [] num_steps = dem_image.shape[0 ] x = np.arange(0 , num_steps) y = np.arange(0 , num_steps) f = RectBivariateSpline(x, y, dem_image / scale_factor) for i in range (num_steps): for j in range (num_steps): theta = theta_start - i / num_steps * delta_theta phi = phi_start + j / num_steps * delta_phi xnew, ynew = sphere2plane(theta, phi) r = ( f( xnew - row * (num_steps - pre_padding[0 ]), ynew - col * (num_steps - pre_padding[1 ]), )[0 , 0 ] + radius ) x = r * cos(theta) * cos(phi) y = r * cos(theta) * sin(phi) z = r * sin(theta) vertices.append((x, y, z)) faces = [] for i in range (num_steps - 1 ): for j in range (num_steps - 1 ): current = i * num_steps + j next_theta = current + num_steps faces.append([current, next_theta, current + 1 ]) faces.append([current + 1 , next_theta, next_theta + 1 ]) sphere_segment = mesh.Mesh(np.zeros(len (faces), dtype=mesh.Mesh.dtype)) for i, f in enumerate (faces): for j in range (3 ): sphere_segment.vectors[i][j] = vertices[f[j]] sphere_segment.save(output_path) if __name__ == "__main__" : path = "/disk527/DataDisk/a804_cbf/datasets/lunar_crater/Lunar_LRO_LOLAKaguya_DEMmerge_60N60S_512ppd.tif" output_dir = "/disk527/sdb1/a804_cbf/datasets/lunar_crater" base_batch = 960 num_batches = LINES // base_batch num_samples = LINE_SAMPLES // base_batch delta_theta = 2 / 3 * pi / num_batches delta_phi = 2 * pi / num_samples radius = 1737.4 * 1000 / scale_factor print ( f"The basic batch of DEM is {base_batch} x{base_batch} . Each line contains {num_samples} batches. There are totally {num_batches*num_samples} basic batches." ) with open (path, "rb" ) as f: line = f.read(LABEL_BYTES) padding = [1 , 1 ] for row in tqdm.tqdm(range (num_batches)): if row == 0 : data = f.read(LINE_SAMPLES * BYTES_PER_PIXEL * (base_batch + 1 )) data_array = np.frombuffer(data, dtype=np.int16).reshape( base_batch + 1 , LINE_SAMPLES ) strip = data_array[-1 , :] delta_theta_start = 0 elif row == num_batches - 1 : data = f.read(LINE_SAMPLES * BYTES_PER_PIXEL * (base_batch - 1 )) strip = data_array[-2 :, :] data_array = np.frombuffer(data, dtype=np.int16).reshape( base_batch - 1 , LINE_SAMPLES ) data_array = np.vstack((strip, data_array)) delta_theta_start = -delta_theta * 2 / base_batch else : data = f.read(LINE_SAMPLES * BYTES_PER_PIXEL * base_batch) strip = data_array[-1 , :] data_array = np.frombuffer(data, dtype=np.int16).reshape( base_batch, LINE_SAMPLES ) data_array = np.vstack((strip, data_array)) delta_theta_start = -delta_theta / base_batch if not os.path.exists(os.path.join(output_dir, "dem_int16" )): os.makedirs(os.path.join(output_dir, "dem_int16" )) if not os.path.exists(os.path.join(output_dir, "stl_models" )): os.makedirs(os.path.join(output_dir, "stl_models" )) if not os.path.exists(os.path.join(output_dir, "dem_int16" , f"{row} " )): os.makedirs(os.path.join(output_dir, "dem_int16" , f"{row} " )) if not os.path.exists(os.path.join(output_dir, "stl_models" , f"{row} " )): os.makedirs(os.path.join(output_dir, "stl_models" , f"{row} " )) for col in range (num_samples): if col == num_samples - 1 : img_array = data_array[ :, col * base_batch - 1 : (col + 1 ) * base_batch ] delta_phi_start = -delta_phi / base_batch else : img_array = data_array[ :, col * base_batch : (col + 1 ) * base_batch + 1 ] delta_phi_start = 0 theta_start = pi / 3 - (delta_theta * row + delta_theta_start) phi_start = delta_phi * col + delta_phi_start create_sphere_segment( img_array, row, col, radius, theta_start, delta_theta, phi_start, delta_phi, padding, os.path.join( output_dir, "stl_models" , f"{row} " , f"{row} _{col} _{base_batch} .stl" , ), )