第一篇文献

MetaEarth: A Generative Foundation Model for Global-scale Remote Sensing Image Generation

解决的问题

本文是将扩散模型用于遥感领域的超分辨率解决方案，专门解决遥感图像领域数据集不足、下游任务训练难以拟合的问题。

主要内容

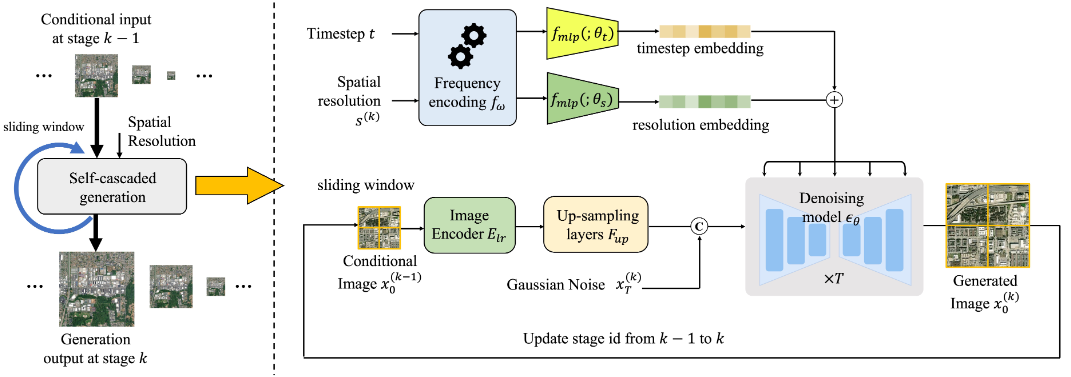
本文在DDPM的工作框架基础上，增加了两点修改方案以改善遥感图像生成所要求的连续性和有意义性质：

  1. 基于DDPM的扩散生成框架通常只对时间变量tt作编码embedding，本文将这一步扩展至对分辨率作编码；
  2. 为了保证生成的遥感图像在空间上连续，本文将前一位置生成的图像作为条件控制量，将其拆分为两部分（从左和从右），分别作图像生成，并根据相同部分拼接在一起，实现无缝图像生成；
    。其工作数据流如下所示：
    遥感图像生成
    本文主要使用了超分辨率的方法，其中值得注意的一点是，超分是先作一次上采样后加入高斯噪声作条件生成。超分前后，生成图像在像素级别上平滑。

文章仅使用了8块4090完成数据并行训练，共计训练2000GPU小时（约5天）。

方法评价

本文算是将扩散模型应用至遥感图像数据集生成的一次尝试，从无到有完成扩散模型的训练，取得了不错的生成效果。但是文章也仍然有较多的问题：第一，缺乏消融实验，尤其是对自己新增加的分辨率编码模块，尚未使用消融实验证实该模块的作用，而消融实验仅对分辨率生成中的条件引导项作实验，而显然该项是必不可少的；第二，文章事实上只是一个超分辨模型，专用于数据集生成，而不是对真实物理世界的超分辨率，文章题目和摘要在这里具有明显的歧义，展现出不专业。

第二篇文献

Improved Denoising Diffusion Probabilistic Models

解决的问题

本文是DDPM的早期改进版本，填补了Ho等人留下的关于DDPM方差不可学习的问题，进一步增强了扩散模型的泛化能力。关于该方差的学习方式，文章采用了巧妙的形式化技巧（类似于KAN的方法）来解决。

主要内容

DDPM原文中使用的噪声模型是椭球高斯分布，即定义为N(μ,σ2(βt)I)\mathcal{N}(\bm{\mu},\sigma^2(\beta_t)\mathbf{I})，本文将椭球高斯分布改为任意形式的高斯分布\mathcal{N}(\bm{\mu},\bm(\Simga)(\beta_t))，但是该形式过于自由，学习模型无法收敛。由此本文将该学习的形式修改为：

Σθ(xt,t)=exp⁡[vlog⁡βt+(1−v)log⁡β~t] with β~t=1−αˉt−11−αˉtβt\bm{\Sigma}_\theta(x_t,t)=\exp[\mathbf{v}\log\beta_t+(1-\mathbf{v})\log\tilde{\beta}_t]\text{ with }\tilde{\beta}_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\beta_t

其中，v\mathbf{v}是维度等于图像维度的列向量。文章没有明确说明，推测该向量应该会变成对角矩阵的对角线。计算该方差量训练时，作者在原始损失函数Lsimple=∥ϵt−ϵθ(xt,t)L_\mathrm{simple}=\|\bm{\epsilon}_t-\bm{\epsilon_\theta}(\mathbf{x}_t,t)加上变分下界variation lower bound正则项λLvlb\lambda L_\mathrm{vlb}：

Lvlb=Et∼pt[Ltpt]L_\mathrm{vlb}=\mathbb{E}_{t\sim p_t}\left[\frac{L_t}{p_t}\right]

其中，pt∝E[Lt2]p_t\propto\sqrt{\mathbb{E}[L_t^2]}是理论上各个时间戳处损失的期望值，实际上不能实现，因此作者采用了滑动窗口法0,...,90,...,9近似计算，用均方值作加权值求解期望即可。

方法评价

本文改进了DDPM方差不能学习的问题，增强了扩散模型的泛化能力。在实际应用中，该方法带来的增益在小数据集样本上表现不明显。

第三篇文献

Scalable Diffusion Models with Transformers

解决的问题

本文最早指出了DiT（Diffusion Transformer）的概念，利用Transformer在处理序列数据上的巨大优势，完成图像生成。虽然在这篇文章里面并没有展现出DiT与传统UNet的扩散模型太多区别，因为单幅图像的生成中基本上不存在序列概念，DiT真正发挥优势之处是视频生成和世界模拟器的仿真。

主要内容

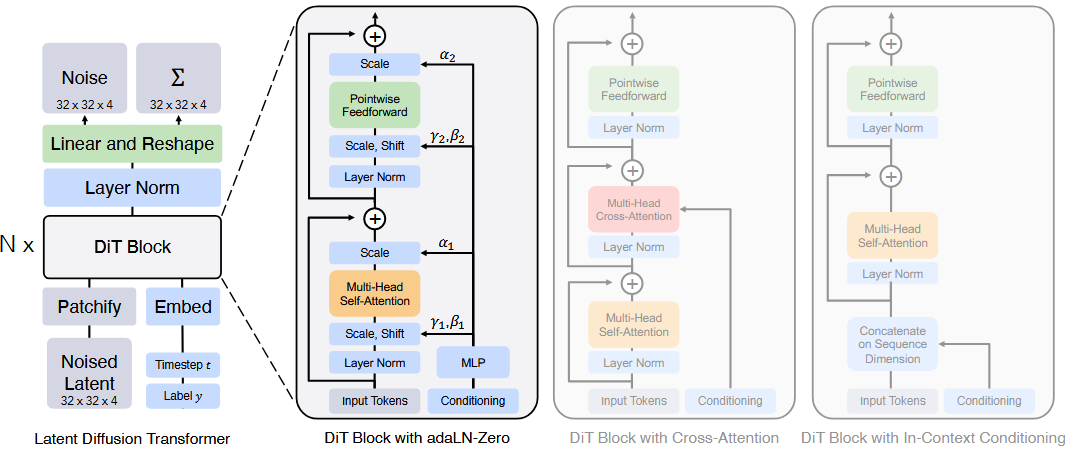
文章指出，UNet结构并不是决定扩散模型在生成式任务上卓越表现的关键因素，因此可以将其替换为时下最为热门的Transform块集合以获取更大的扩展能力scalable。作者将ViT的结构直接用在作计算噪声的噪声估计器，结构如下：
DiT结构
其中的patchify步骤就是ViT最经典的分块位置编码。接下来作者研究了不同形式条件注意力施加形式，包括自适应伸缩、交叉注意力和直接连接，得出结论：在当前应用条件下，似乎自适应伸缩是最有效果的。

方法评价

DiT扩展了扩散模型的使用潜能，Transformer的可拓展性不是UNet能比拟的，但是也带来了相应的问题：即训练的数据量需求将随模型增大而变大，少量的数据样本根本无法完成DiT的训练。

从这一点上看，DiT用于视频领域几乎是必然，因为视频自带很多帧。

第四篇文献

Unsupervised Learning of Visual Representations by Solving Jigsaw Puzzles

解决的问题

本文是无监督学习范式的一次尝试，即如何更多地依据图像之间的像素联系和特征联系，完成对一次打乱后再构建的拼图过程，从而学习到有关于数据集整体表现的特征。

主要内容

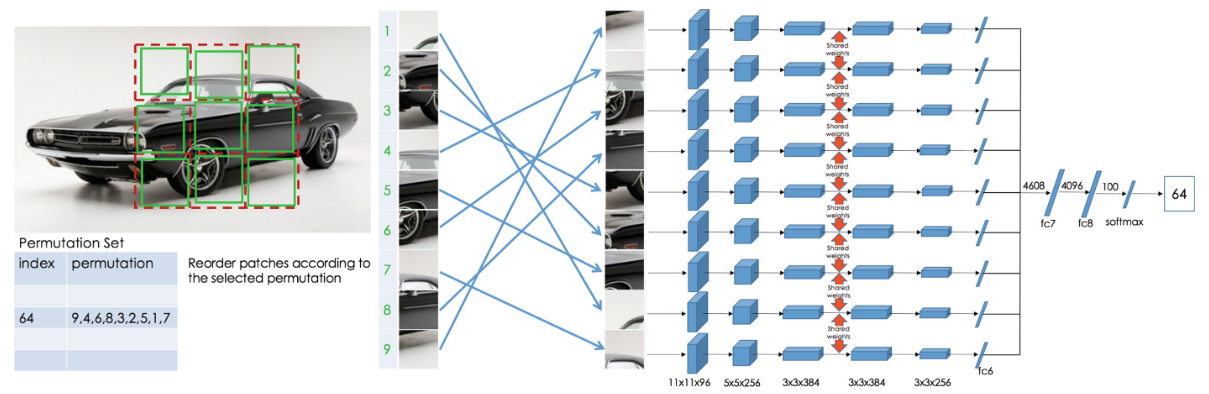
文章提供的拼图网络结构如下图所示：
拼图网络结构示意图
直观上也便于理解，类似于对比学习的两孪生分支Siamese并行，拼图学习的采用九孪生分支并行，接受的输入数据是从原始输入图像上任意获取一个255×255255\times 255的子区域图像，将该子区域9等分，得到75×7575\times75的子图，每块子图再随机获取64×6464\times64分辨率的拼图子块作为输入

这么做的目的是避免训练的网络从边界像素的相邻关系走捷径导致崩塌

从现成的最大汉明距离集合中任意获取一个排列，以该排列作为输入的拼图顺序加入至九孪生网络中，输出分类结果（对应最大汉明距离集合中某个排列的序号，示例中是64）。

关于最大汉明距离集合的生成，因为9拼图的顺序量实在太多（9!=3628809!=362880），实际使用中也没有必要非要选取如此多的排序可能性，因此作者采用了一种偷懒的方式，即随机选取100个汉明距离排列作为预先定义好的最大汉明距离集，并在之后的训练中一直使用这相同的100个排列。

训练完成后的模型与对比学习类似，去除拼图头程序后作为预训练的特征提取器，参与下游视觉处理任务中。

方法评价

本文采取的范式看上去花里胡哨，似乎非常厉害。但是在分类任务上，仍然与AlexNet代表的监督学习（>74>74%）相去甚远，最高能取得57.157.1%，最差仅能38.138.1%，远远比不上对比学习所能达到的6060%甚至7070%。且本文的方法在构建最大汉明距离集合的时候显得过于随意，尚未考虑任意选取的汉明排列是否对结果有影响，100个排列是否足够。文章的消融实现仅和2×22\times2拼图作对比，而未考虑汉明距离集合的基数这一重要因素，因此消融实验不具有较强的说服力。本文提供的范式花哨但是不好用。

第五篇文献

Self-Supervised Learning of Pretext-Invariant Representations

解决的问题

本文与BYOL非常相似，二者的思路也是出奇的一致，都是认为同一幅输入图像在经过不同路径的输入变换后，必定存在某个相对变换保持不变的量，即本文提出的pretext-invariant，自监督预训练所需要执行的就是利用该不变量完成对数据集整体的描述，即完成预训练特征提取。

主要内容

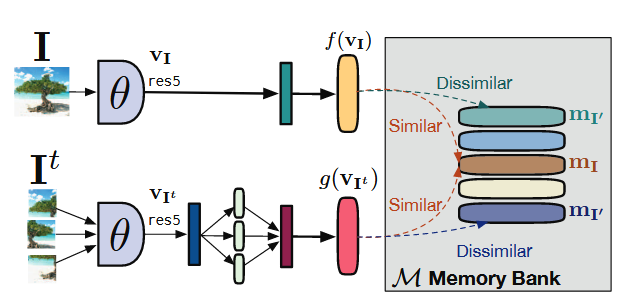
文章提出的训练范式PIRL的示意图如下所示：
PIRL训练范式示意图
与BYOL不同的是，PIRL需要负样本，它在同自身对比的基础上，还需要与负样本对比以保证网络不崩塌。PIRL在加入旋转等基本的变换以外，还将输入的图像拆成大小相同的随机多个子块，经过待取得的特征提取器后合并为与不拆分图像相同的特征向量，然后应用NCELoss作为计算损失的基准，以负样本的数量作为作为正则项，得到以下自对比损失函数形式：

LNCE(I,It)=−log⁡[h(f(vI),g(vIt))]−∑I′∈DNlog⁡[1−h(f(vI),g(vIt))]\mathcal{L}_\mathrm{NCE}(\mathbf{I,I}^t)=-\log[h(f(\mathbf{v_I}),g(\mathbf{v_{I^\mathit{t}}}))]-\sum_{\mathbf{I}'\in\mathcal{D}_N}\log[1-h(f(\mathbf{v_I}),g(\mathbf{v_{I^\mathit{t}}}))]

其中，计算两个矢量对比头的函数为：

h(VI,VIt)=es(VI,VIt)τes(VI,VIt)τ+DNDh(\mathbf{V_I},\mathbf{V_{I^\mathit{t}}})=\frac{e^{\frac{s(\mathbf{V_I},\mathbf{V_{I^\mathit{t}}})}{\tau}}}{e^{\frac{s(\mathbf{V_I},\mathbf{V_{I^\mathit{t}}})}{\tau}}+\frac{\mathcal{D}_N}{\mathcal{D}}}

公式中的s(⋅,⋅)s(\cdot,\cdot)指代的是相似度计算，常见如余弦相似度。DN\mathcal{D}_N是负样本的数量，D\mathcal{D}是样本总数。最终版本的损失函数中还要包括与负样本对比的损失，文中使用λ\lambda加权后整合为一项。

方法评价

本文的方法说对比不对比，说BYOL也不BYOL，不过它在损失函数上的创新是有目共睹的，新加入的类似于对抗的损失函数能够进一步增强对比的能力，且本文能够跳出对图像直接排列的思路定势，用块补丁不变性，避免了拼图汉明距离集合数量有限制约模型表现，因此本文的预训练模型在提取特征上优于上文提到的拼图法。

第六篇文献

DIFFUSION POSTERIOR SAMPLING FOR GENERAL NOISY INVERSE PROBLEMS

解决的问题

本文沿着DDRM的思路，将线性逆问题的扩展至非线性逆，文章指出实际可以使用局部线性化完成非线性逆问题求解，将DDRM能够处理的问题作了扩展。

主要内容

利用随机微分方程写出扩散模型生成过程的表达式：

dx=[−β(t)2x−β(t)(∇xtlog⁡pt(xt)+∇xtlog⁡pt(y∣xt))]dt+β(t)dw\mathrm{d}\mathbf{x}=\left[-\frac{\beta(t)}{2}\mathbf{x}-\beta(t)\left(\nabla_{\mathbf{x}_t}\log p_t(\mathbf{x}_t)+\nabla_{\mathbf{x}_t}\log p_t(\mathbf{y|x}_t)\right)\right]\mathrm{d}t+\sqrt{\beta(t)}\mathrm{d}\mathbf{w}

恢复模型将条件量定义为：

y=A(x0)+n\mathbf{y=\mathcal{A}(x_\mathrm{0})+n}

实际上与非线性相关的且不好计算的量是∇xtlog⁡pt(y∣x)\nabla_{\mathbf{x}_t}\log p_t(\mathbf{y|x})，传统模型则想方设法在局部小邻域内将非线性问题线性化，从而得到上式的近似解，本文没有采用这一路径，而是利用詹森不等式引出的詹森差E[f(x)]−f(E(x))\mathbb{E}[f(\mathbf{x})]-f(\mathbb{E(\mathbf{x})})将该项约束到上界，由此得到约束结果：

∇xtlog⁡p(y∣xt)≈∇xtlog⁡p(y∣x^0)\nabla_{\mathbf{x}_t}\log p(\mathbf{y|x}_t)\approx\nabla_{\mathbf{x}_t}\log p(\mathbf{y|\hat{x}}_0)

从而产生近似的解析解，解决了不同时间步条件概率不好求的问题。常见如高斯噪声，可表示为：

p(y∣x0)=1(2π)nσ2nexp⁡(−12σ2∥y−A(x0)∥22)p(\mathbf{y|x}_0)=\frac{1}{\sqrt{(2\pi)^n\sigma^{2n}}}\exp\left(-\frac{1}{2\sigma^2}\|\mathbf{y-A(x}_0)\|^2_2\right)

由此可完成条件引导的噪声估计。

方法评价

本文采用的方式相比局部小邻域线性化，更加稳健，但是由于詹森不等式受限于凸函数的取值，上界的约束关系在不同的位置处不一定能够取得相同的值，因此生成模型的结果仍然存在不可控因素。