8月以来经历了暑假放假，中间迷惘一周，大致于8月16号之后才正式进入状态。

第一篇文献

Event-Based Motion Magnification

解决的问题

本文将事件相机用于高速摄影，本质上仍然是一种新型的事件流插帧方式，解决了在高频振动测量领域的高速摄影问题。

主要内容

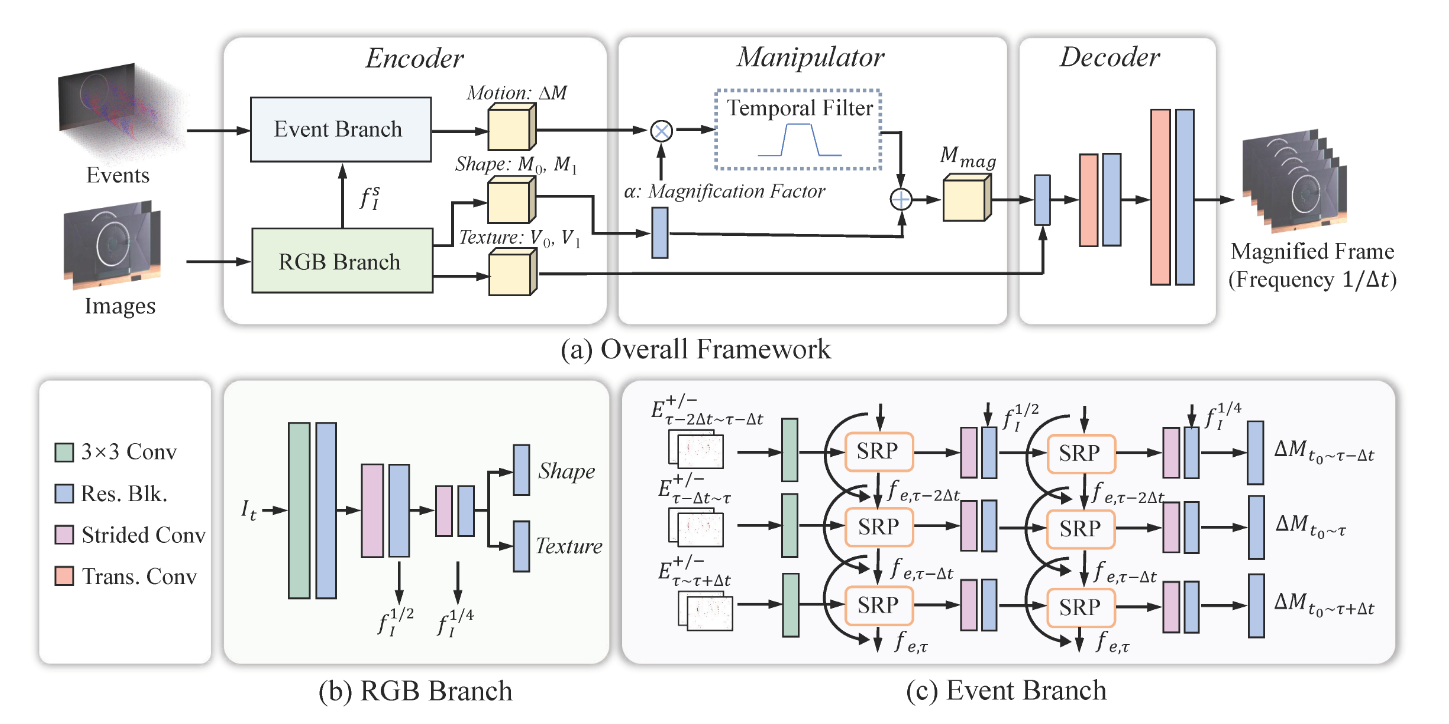
非最新的事件流插帧算法往往不能处理高频振动这种具有典型周期性的特征，其重建结果难以准确描述高频振动的音叉边缘外形，作者利用事件相机的高速摄影性能，将音叉的高频振动用事件流的放大。使用事件流重建图像时，使用了事件的对数微分性质，因此重建图像时将其积分后求指数，即有：

$I(\mathbf{u})=I_0(\mathbf{u})\exp\left(c\int_{t_0}^\tau p(\mathbf{u},t)\right)$

其中 $\mathbf{u}$ 是图像 $I$ 的某个位置， $\tau$ 是插帧时刻。利用上式，可以在一阶近似的意义下解出高频振动场的像素亚像素精度运动，该部分原理构成了下图网络中的SRP（Second-order Recurrent Propagation）环节：
事件相机运动放大
网络的训练损失，作者选用了RMSE，但是在根号项中增加了一项惩罚项 $\epsilon$ ，得到如 $\sqrt{\|\hat{x}-\hat{x}\|^2 +\epsilon^2}$ 的式子，分别将 $x$ 替换为像素灰度 $\mathcal{L}_r$ 、纹理值 $\mathcal{L}_t$ 、事件运动量 $\mathcal{L}_s$ ，三者加权即得最终的损失函数。

方法评价

本文的方法在插帧领域惯用的技术手段基础上，增加了关于周期性的约束，由此出色完成了高频振动条件下的周期外形测量任务。该方法提到了事件相机用于摄影测量的重要基础：事件积分，凡是需要使用事件流的作测量的任务，该式子都将有相当重要的参考意义。

第二篇文献

Structure-from-motion revisited

解决的问题

本文是大名鼎鼎的位姿解算与三维重建基础软件COLMAP的理论依据，充分解决了多视图几何中关于三维重建和位姿解算的问题，提供了一整套闭环方法论和开源软件，当之无愧的三维重建和位姿解算领域祖师爷级别的论文。

主要内容

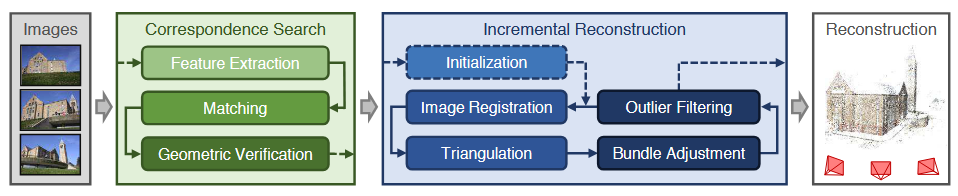
运动结构估计Structure from Motion是使用多个不同视角处的同一物体照片，解决相机当前位置姿态解算和物体三维点重建。其完成的工作流如下图所示：
COLMAP工作流
COLMAP用到了前述关于机器学习、数学领域多个成果，其关键的创新点在于：

归纳、总结了增量式重构的工作流，提出了完整的三维重构闭环算法；
优化了场景图像匹配算法，解决了图像匹配算法不够稳定的问题，称为场景图增强Scene Graph Augmentation；
优化了增量重构的设计思路，着重解决了如何选取图像进行下一帧的匹配、三角测量的问题，称为最优下一帧选择Next Best View Selection；
优化了三角测量的计算复杂度，并取得了更加稳健的计算结果；
逐步使用光束法平差，保证了三维重建空间点的稳定性；
优化了光束法平差的换元思路，能够从富余的场景图像中获取稠密空间点。

文章信息量极高，下文分工作流部分和创新点部分展开叙述。

COLMAP工作流详述

COLMAP的工作流程主要分为两个步骤：关联查找和增量重构。

关联查找

本步骤类似于传统的多视图几何的特征点对匹配，即建立不同图像中同一个点的关系。通过三个主要的步骤：

特征提取：支持用户自定义角点算子或其他类似不变量的算子，保持射影变换不变即可。
匹配：内置基于简单相似度测度的匹配法（时间复杂度将达到 $O(m^2n^2)）$ ，同时也支持相当数量的衍生匹配算法。
几何校正：利用单应性变换、对极几何或者三焦点张量校正图像对的匹配点对，使用RANSAC保证匹配点对都是内点inliers，去除噪声点和非射影变换因素。

关联查找最终的输出结果是两幅几何校正后的图像对 $\mathcal{\bar{C}}$ ，两幅图像上对应点 $\mathcal{\bar{M}}_{ab}$ ，两幅图像可能的位置关系 $\mathcal{G}_{ab}$ 。

增量重构

增量重构使用关联查找输出的三个量 $\mathcal{\bar{C}},\mathcal{\bar{M}}_{ab},\mathcal{G}_{ab}$ 作为输入，通过以下步骤完成三维重建：

初始化：由于BA算法需要输入初始位姿估计，COLMAP选择采用两视图重构，算法将查找全部可能的图像对，选取其中对应点数量最多的，以获取稳健的初始位姿估计。
图像配准：即图像点与空间点的PnP过程，此时仍然需要保证投影结果是内点有效的，因此需要应用RANSAC，逐图像地与空间点作配准。
三角测量：新加入的图像可能会观察到当前三维空间点中不存在的点（例如某些视角下被遮挡的点），配准结果将保证新加入的三维点能够被判定为有效，同时加入至三维重建点集 $\mathcal{X}$ 中。
光束法平差：基于最小二乘原理的PnP算法将在某些点处产生极高的病态结果，影响三维点的生成质量，COLMAP将隔一段图像进行一次全局BA，优化其非线性误差 $\sum_j\rho_j\left(\|\pi(\mathbf{P}_c,\mathbf{X}_k)-\mathbf{x}_j\|^2_2\right)$ 。

创新点说明

以上工作流并不是文章的原创，但是能把它总结得如此清晰已然是高水平，此外，本文还提出了更加重量级的创新内容。

场景图增强

本方法能够应对输入的图像存在诸如水印、时间戳或者边框等不良信息，利用匹配的两幅图像获取的匹配点对计算估计的单应性变换，排除其中重投影误差的点对。然后，在图像的边框位置单独再查找外点数量，当外点个数超过超参数阈值后，认为该图像的质量堪忧，应当从三维重建的图像数据库中剔除。经过场景图增强后的图像对中含有的均为有效内点，较高噪声的外点和错误的假点均被舍去。

最优下一帧选择

由于BA算法是典型的非线性优化，PnP算法对选取的图像位姿又较为敏感，因此参与重建的匹配图像选取将显著地影响三维重建精度。作者选取与当前三维点重叠程度较高（对图像作 $K_l$ 的重采样，用含有重投影点的重采样网格作为有效网格，统计有效网格的个数）的新图像作为下一帧候选，如该图像的关键点分布较为均匀，则将该帧图像作为最优下一帧。

稳健三角化

在保证三角测量的配对特征点视场角 $\alpha$ 大于某个给定阈值后，将匹配的图像对之内的全部关键点作一次随机采样一致性判断以去除重投影偏离量较大的点。

光束法平差

本文选用的光束法优化函数为柯西函数 $\rho(x)=-\log[\exp(-\frac{1}{2}x^2)+\epsilon]$ ，能够更加稳健地提供优化梯度。平差前后，仅对新加入的三维候选点作平差，减轻平差计算器的负担。平差计算后再次进行三角测量Re-Trianglization,RT，检查每个点的重投影误差，现次去除多余点和噪声点。最后，迭代地精调全部三维点，即迭代使用RT排除其中的外点，直到外点数量收敛，此时得到的三维重建结果精度极高。

说明

文章最后还提到了一个称为冗余视角提炼的方法，似乎是用来对高度重复的场景信息作按视角的分类，以期望在不同的视角内单独优化获取更加精准的重建信息和相机位姿。

方法评价

经典之作，当前仍然沿用不休。提供的思维设计充分展现了系统工程的能力，设计系统如能保证闭环稳定，往往能够取得比单向传递更加优良的测量结果，这是本文带给我的最大收获。

第三篇文献

SuperPoint: self-supervised interest point detection and description

解决的问题

本文提出了一种基于自监督学习的高效关键点提取、匹配方法，能够直接从两视角图像对中获取有效的匹配关键点，为后续诸如相机位姿信息解算或者空间三维重建任务提供大量有效的特征点。

主要内容

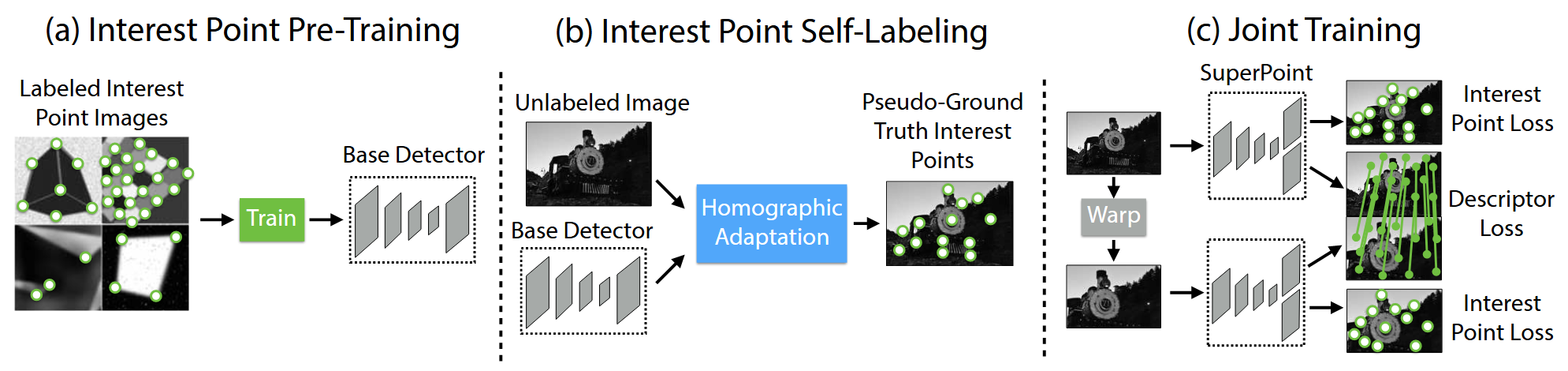
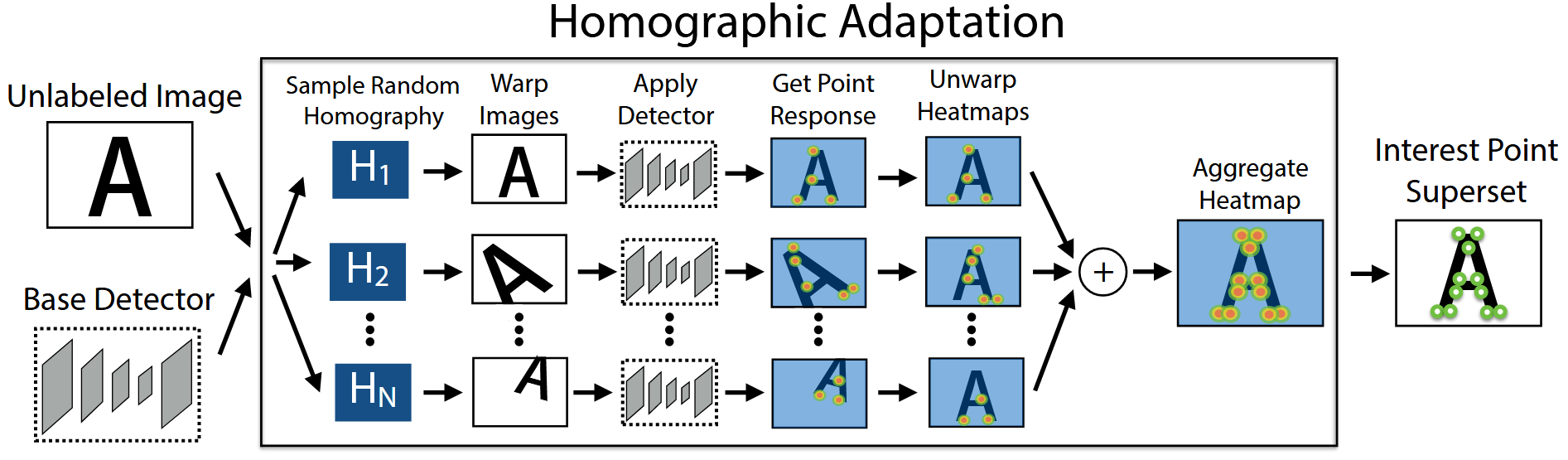
本文的思路类似于迁移学习，又借鉴了表征学习领域中自监督设计思路。首先从简单的、外形鲜明的几何特征图像中直接获取特征点，预训练网络从图像中提取角点的能力。然后，从输入的自然图像中调用预训练模型，选取某个已知的单应性变换，对图像作一次单应变换，由此产生一定数量的准GT关键点，最后，根据已知的单应性变换信息和变换前后的关键点对应关键，计算描述损失完成网络优化，其工作流程如下图所示：
SuperPoint工作流
关键点提取网络的设计采用卷积编码-解码器网络在高维隐空间中计算特征。关于匹配点对的损失函数，文章使用了以下两种类型的损失：

配对损失（文章称为点损失 $\mathcal{L}_p$ ）：计算配对点的NCE Loss，其中负样本的个数为65个。
描述损失 $\mathcal{L}_d$ ：计算两个匹配图像上的图像点的位置误差（且仅计算潜在的匹配点，不是匹配点的舍去）。

训练后的网络，可经一次自适应单应变换获取足够多的关键点，如下图所示：

实验结果表明，本文能够取得比传统SIFT算子更多的关键点，且计算用时不高，在CPU上作一次1000点的计算，平均每点用时1.5ms。

方法评价

本文提供了一种全机器学习的关键点检测与匹配算法，直接解决了三维重建或位姿解算领域的数据输入问题。文章设计的网络也遵循了一般的自监督范式，不需要人工标注数据集，使用起来方便可靠。

第四篇文献

EMVS: event-based multi-view stereo—3D reconstruction with an event camera in real-time

解决的问题

本文是早期的事件相机应用文献，考察了如何在仅使用事件相机的前提下，使用事件点完成空间点的三维重建，并由此给出了详细完整的数学方法论。

主要内容

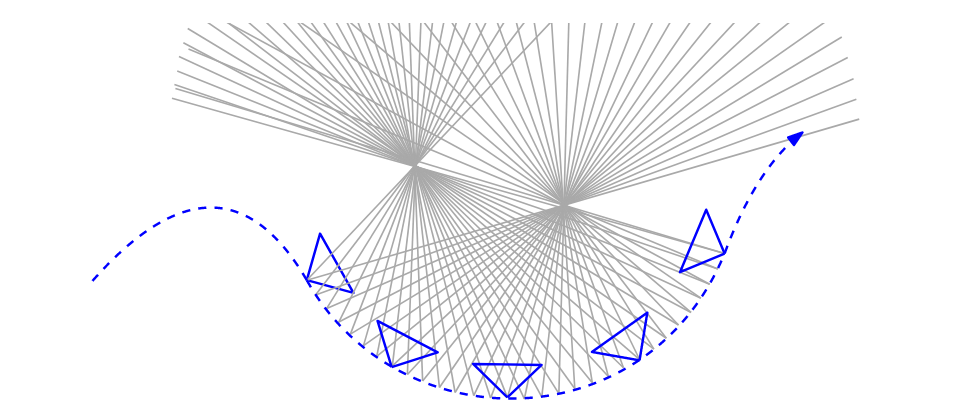
多视图几何是机器视觉领域引以为傲的应用，集成了机器视觉领域全部的关键技术。其特点是：需要多幅图像及其对应特征点，由三角测量原理，对应特征点与基线的深度距离可以被测定。事件相机并不能得到图像一样稠密的像素点，并同时失去了灰度这一常用的匹配信息，因此直接采用诸如SuperPoint等点匹配方式的三维重建是行不通的，本文作者另辟蹊径，用光线密度法完成稀疏事件点的三维重建。如下图，首先需要已知各个时间处的相机投影矩阵 $\mathbf{P}$ （即相机位姿需要先验确定），每个位置处的事件点 $\mathbf{e}$ 均可使用 $\mathbf{P}$ 反投影为空间向量 $\mathbf{\tilde{n}}$ 。
事件点光线反投影

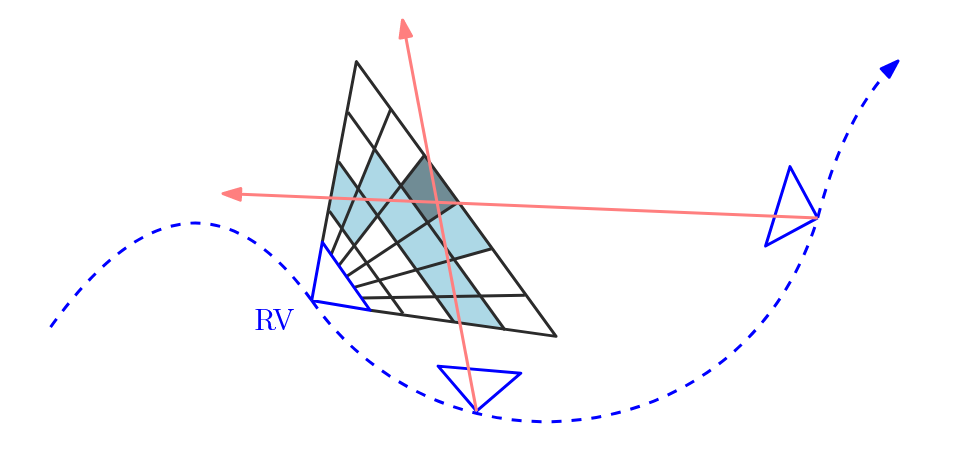
文章选取一定数量的事件点 $N$ ，假定在这段事件流内，相机的运动很轻微，可近似认为当前事件流中全部点均由同一个摄像机矩阵 $\mathbf{P}_k$ 产生，（对应于选取一段较短的采样时间间隔 $t_k,t_k+\delta t$ ）。齐次图像点反投影得到的三维方向向量从当前相机中心出发，弥散至整个空间，此时，由于事件流的产生是出现于边缘位置处，即当噪声水平适度的情况下，大多事件流中的点均是对应某些相同的位置（例如三维物体的边角），因此，当相机产生微小位置和旋转后，反投影向量仍然会经过这些关键点，造成在关键点附近的光线密度增加。文章对于如何度量这样的密度，使用的方法是投影空间网格采样，如下图所示：

在某个假定位置处设置一个采样平面，将其逐深度反投影至空间中得到多层反投影采样网格。由于深度大的地方发出的光线更难以被相机投射，因此采样网格尺寸将随投影深度的增加而变大，以便于适应深度保证采样点均匀分布。具体的实现算法中提到了从某个深度为0的参考虚平面出发，逐深度采样。最终，统计落在各个采样网格内的光矢量个数，确定该网格内是否存在三维点。

方法评价

本文的方法很充分地利用了事件流前后高度关联的信息，用反投影矢量的密度作为判断是否存在三维点的方法也能够允许更多的重建机会。但是先验信息需要已知姿态信息，事实上仍然有较大的应用限制。且重建的网格在整个空间中并不均匀，当相机运动的轨迹稍大，重建容易失败。

第五篇文献

CraterDANet: A Convolutional Neural Network for Small-Scale Crater Detection via Synthetic-to-Real Domain Adaptation

解决的问题

本文是陨石坑检测领域的迁移学习范式，即如何平衡仿真陨石坑与真实陨石坑图像对检测算法的应用差异，同时提供了一种基于合成图像的光照迁移算法，以获取更加逼真的合成陨石坑图像。

主要内容

本文提出的陨石坑模型为：

$\begin{aligned} \Delta h &= k\left[\left(\frac{d}{r^2}-\frac{1}{4}\right)r\right]\left(1-\frac{d}{r}\right)\\ d &= \sqrt{(x-x_c)^2+(y-y_c)^2} \end{aligned}$

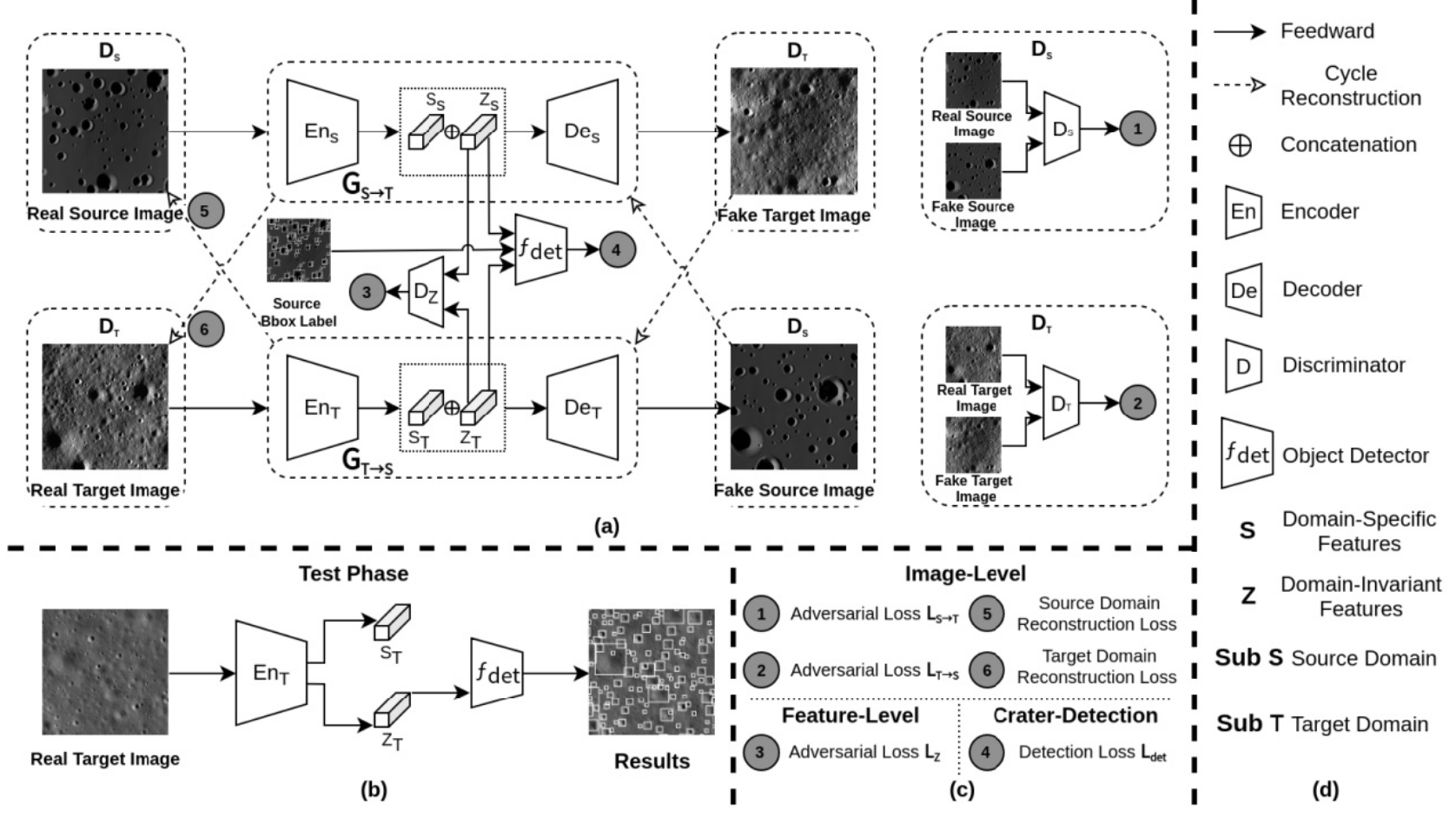
其中 $\Delta h$ 为陨石坑深度， $k$ 为陨石坑深度系数， $d$ 为陨石坑中心到某点的距离， $r$ 为陨石坑半径， $(x_c,y_c)$ 为陨石坑中心坐标。基于该模型，本文预设光照仿真生成陨石坑。交叉使用真实图像与仿真图像作为训练集，用训练结果交叉反向传播修改模型参数，如下图所示：
陨石坑迁移学习示意图
训练使用的损失函数是典型的迁移学习损失类型，即GAN损失、回传损失，然后加入检测模型的损失即位置损失和标签损失。测试时，不再使用仿真的数据集以保证网络对真实陨石坑图像的泛化能力。

方法评价

本文提供了从仿真数据集向真实数据集的泛化迁移模块，同时也提出了一种新的陨石坑仿真生成方法。实际上，如果真的要得到高质量的仿真图像，使用扩散模型将是更有效、更便携的方式。唯一不能解决的是，扩散模型得到的陨石坑没有标注，需要重新手工标注。本文的迁移目的不明确，有凑论文的嫌疑。